BASIC STEPS TO CALCULATE THE CENTER OF GRAVITY
Basic steps to calculate the center of gravity:
General:
The term arm, usually measured in inches, refers to the distance between the center of gravity of an item or object and the datum. Arms ahead of, or to the left of the datum are negative (-), and those behind, or to the right of the datum are positive (+). When the datum is ahead of the aircraft, all of the arms are positive.
The datum may be located anywhere the manufacturer chooses; it is often the leading edge of the wing or some specific distance from an easily identified location. One popular location for the datum is a specified distance forward of the aircraft, measured in inches from some point, such as the nose of the aircraft, or the leading edge of the wing, or the engine firewall.
Relationships between the algebraic signs of weight, arms, and moments..
Steps to calculate moment, CG
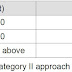
The lever is balanced when the algebraic sum of the moments is zero. Consider these facts about the lever in Picture 1, we can display in tabular form as below:
Determining the CG
One of the easiest ways to understand weight and balance is to consider a board with weights placed at various locations. We can determine the CG of the board and observe the way the CG changes as the weights are moved.
The CG of a board like the one in picture 1 may be determined by using these four steps:
- Measure the arm of each weight in i:q. 4es from the datum.
- Multiply each arm by its weight in pounds to determine the moment in pound-inches of each weight.
- Determine the total of all weights and of all the moments. Disregard the weight of the board.
- Divide the total moment by the total weight to determine the CG in inches from the datum.
In picture 2, the board has three weights, and the datum is located 50 inches to the left of the CG of weight A.
Determine the CG by making a chart with data in picture 2.
To prove this is the correct CG, move the datum to a location 110 to the right of the original datum and determine the arm of each weight from this new datum, (as in picture 3). Then make a new chart. If the CG is correct, the sum of the moments will be zero.
Determining the CG of an airplane is done in the same way as determining the CG of the board in the previous example. The example below show the way to calculate the aircraft CG
The empty weight of this aircraft is 5,862 pounds. Its EWCG, determined by dividing the total moment by the total weight, is located at fuselage station 201.1. This is 201.1 inches behind the datum.
Shifting the CG
One common weight and balance problem involves moving passengers from one seat to another or shifting baggage or cargo from one compartment to another to move the CG to a desired location.
To shift weight B so the board will balance about its center, 50 inches from the CG of weight A, first determine the arm of weight B that will produce a moment that causes the total moment of all three weights around this desired balance point to be zero. The combined moment of weights A and C around this new balance point, is 5,000 in-lb, so the moment of weight B will have to be -5,000 lbin in order for the board to balance.
Determine the arm of weight B by dividing its moment, -5,000 lb-in, by its weight of 200 pounds. Its arm is -25 inches.
Arm B = Moment
Weight
= -5,000
200
= -25
To balance the board at its center, weight B will have to be placed so its CG is 25 inches to the left of the center of the board,
General:
The term arm, usually measured in inches, refers to the distance between the center of gravity of an item or object and the datum. Arms ahead of, or to the left of the datum are negative (-), and those behind, or to the right of the datum are positive (+). When the datum is ahead of the aircraft, all of the arms are positive.
The datum may be located anywhere the manufacturer chooses; it is often the leading edge of the wing or some specific distance from an easily identified location. One popular location for the datum is a specified distance forward of the aircraft, measured in inches from some point, such as the nose of the aircraft, or the leading edge of the wing, or the engine firewall.
Relationships between the algebraic signs of weight, arms, and moments..
Steps to calculate moment, CG
The lever is balanced when the algebraic sum of the moments is zero. Consider these facts about the lever in Picture 1, we can display in tabular form as below:
Determining the CG
One of the easiest ways to understand weight and balance is to consider a board with weights placed at various locations. We can determine the CG of the board and observe the way the CG changes as the weights are moved.
The CG of a board like the one in picture 1 may be determined by using these four steps:
- Measure the arm of each weight in i:q. 4es from the datum.
- Multiply each arm by its weight in pounds to determine the moment in pound-inches of each weight.
- Determine the total of all weights and of all the moments. Disregard the weight of the board.
- Divide the total moment by the total weight to determine the CG in inches from the datum.
In picture 2, the board has three weights, and the datum is located 50 inches to the left of the CG of weight A.
Determine the CG by making a chart with data in picture 2.
To prove this is the correct CG, move the datum to a location 110 to the right of the original datum and determine the arm of each weight from this new datum, (as in picture 3). Then make a new chart. If the CG is correct, the sum of the moments will be zero.
Determining the CG of an airplane is done in the same way as determining the CG of the board in the previous example. The example below show the way to calculate the aircraft CG
The empty weight of this aircraft is 5,862 pounds. Its EWCG, determined by dividing the total moment by the total weight, is located at fuselage station 201.1. This is 201.1 inches behind the datum.
CG = Total moment
Total weight
= 1,179,057
5,862
= 201.1 inches behind the datum
Shifting the CG
One common weight and balance problem involves moving passengers from one seat to another or shifting baggage or cargo from one compartment to another to move the CG to a desired location.
To shift weight B so the board will balance about its center, 50 inches from the CG of weight A, first determine the arm of weight B that will produce a moment that causes the total moment of all three weights around this desired balance point to be zero. The combined moment of weights A and C around this new balance point, is 5,000 in-lb, so the moment of weight B will have to be -5,000 lbin in order for the board to balance.
Determine the arm of weight B by dividing its moment, -5,000 lb-in, by its weight of 200 pounds. Its arm is -25 inches.
Arm B = Moment
Weight
= -5,000
200
= -25
To balance the board at its center, weight B will have to be placed so its CG is 25 inches to the left of the center of the board,
BASIC STEPS TO CALCULATE THE CENTER OF GRAVITY
 Reviewed by Aviation Lesson
on
12:23 AM
Rating:
Reviewed by Aviation Lesson
on
12:23 AM
Rating:
 Reviewed by Aviation Lesson
on
12:23 AM
Rating:
Reviewed by Aviation Lesson
on
12:23 AM
Rating:














No comments: